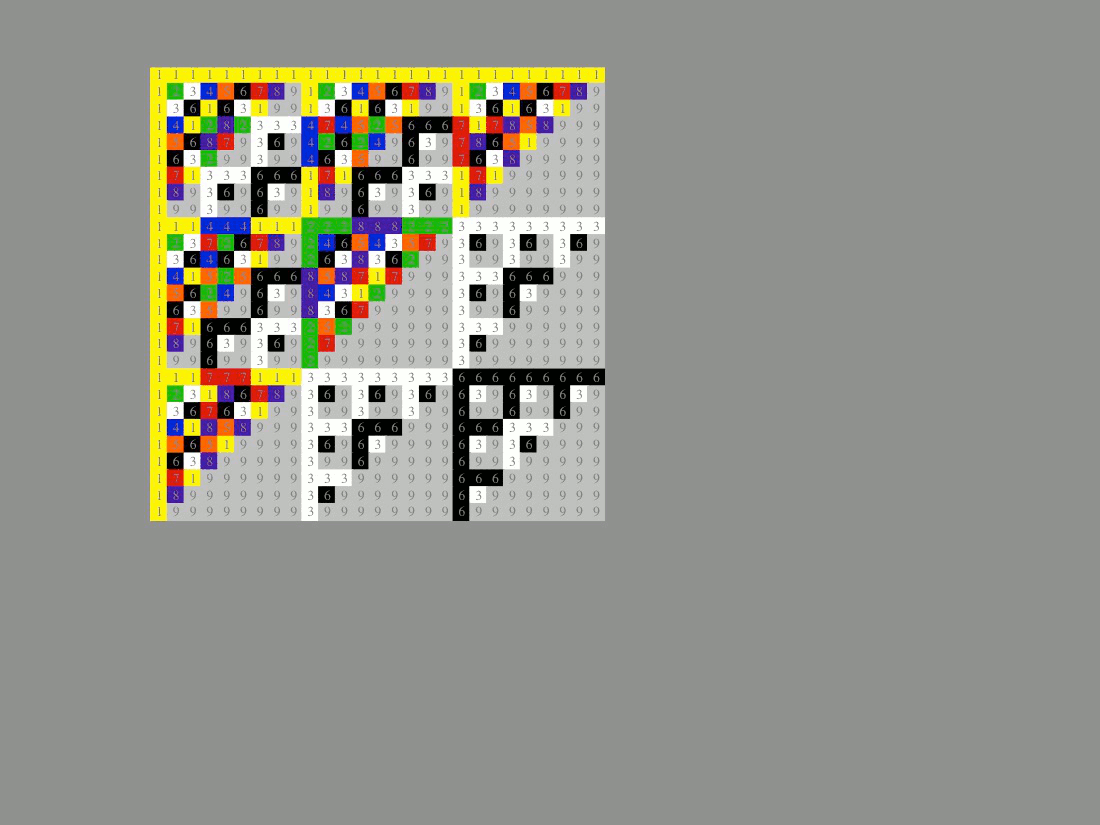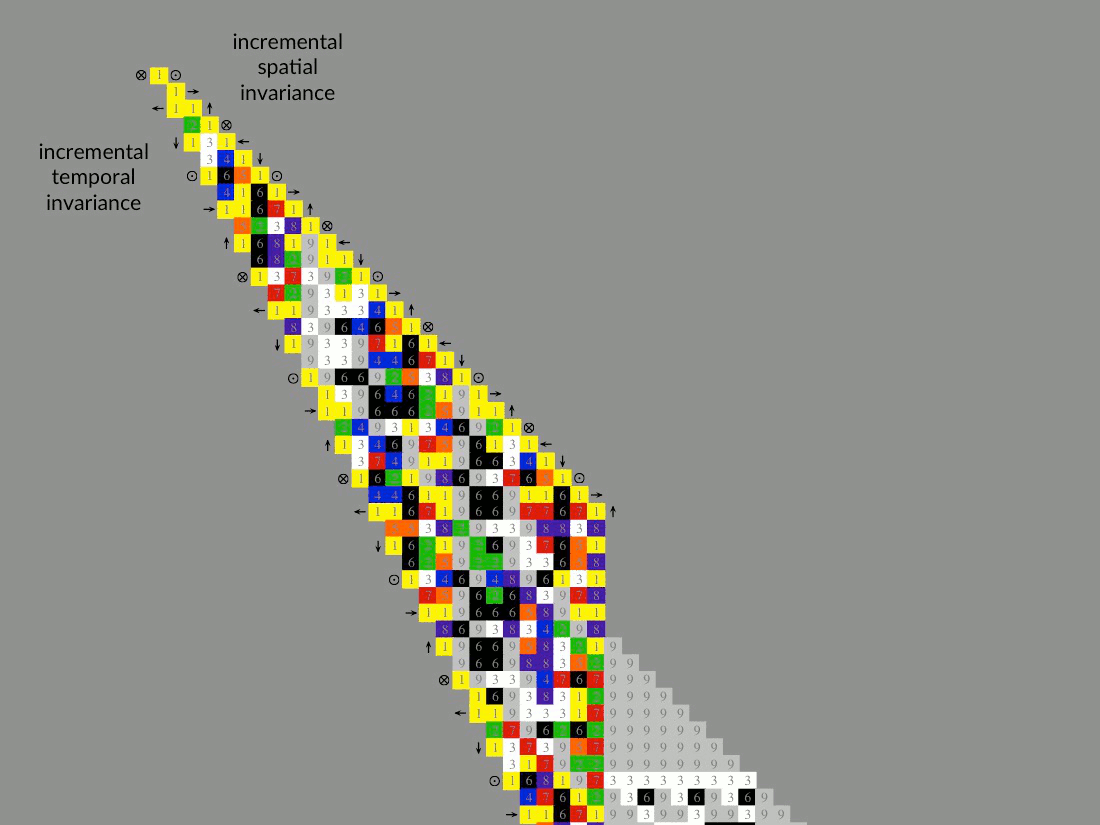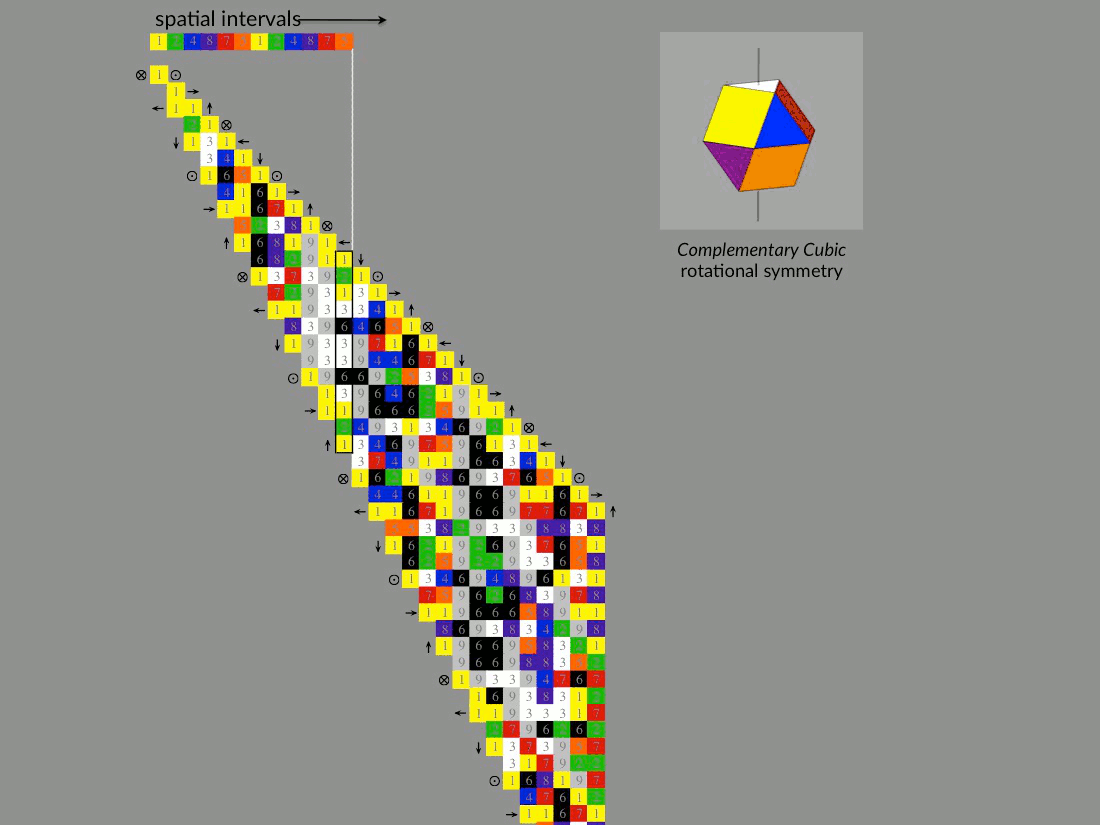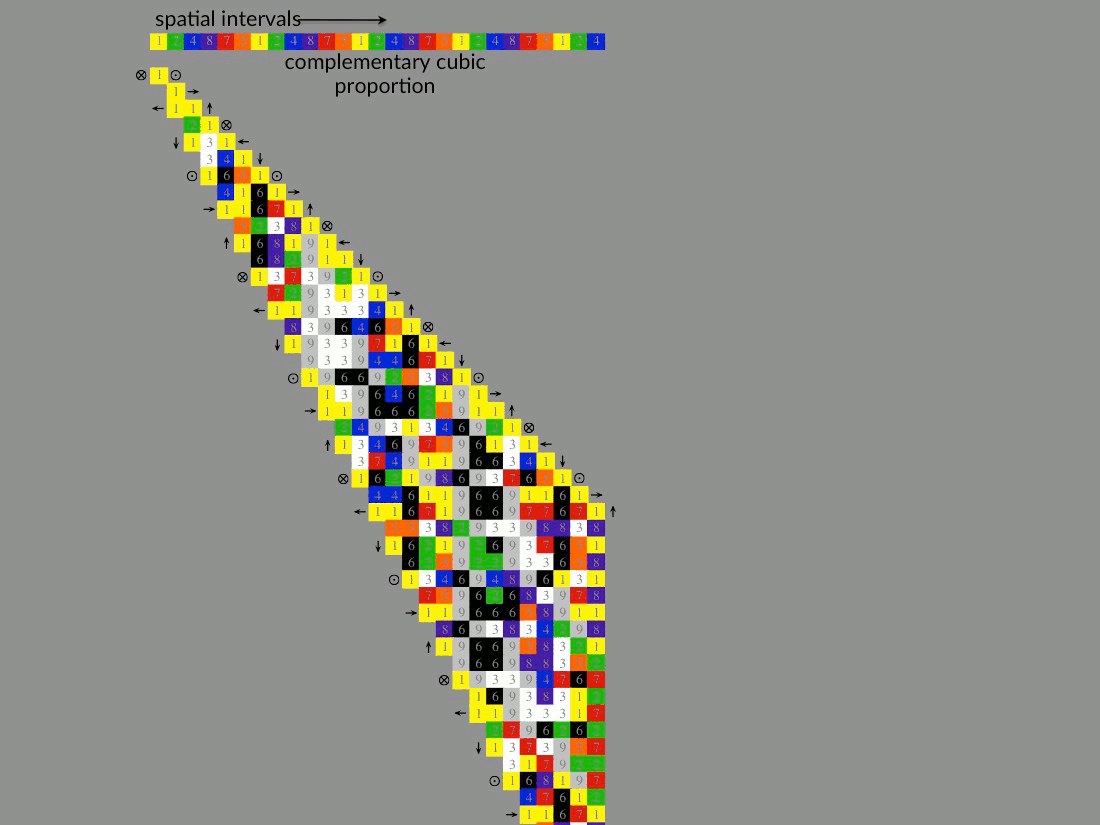The universe is one, and it began to come into being from the center, and from the center upwards at the same intervals as those below. For the parts above from the center are in inverse relationship to those below; for both stand in the same relationship to the center, except in so far as their positions are reversed.
Philolaus
Welcome to the Natural Number animation page. Here you’ll find several amazing animated visualization aids that underscore essential elements of dimensional number theory. Explore the unified spatial/temporal dimensional geometry of Pascal’s triangle as it evolves through the rotational symmetry transformations of its continuous golden proportion (the Fibonacci series) — transformations revealed through analysis of the accompanying complementary modulus 9 number symmetry. For more complete treatment of these fundamental natural numeric phenomena explore Chapters 3 thru 9 in conjunction with this page.

Triangular Number, mod 9, and the close packing of concentric spheres…
Use the adjacent animation to explore the geometric relationship between the triangular number series and modulus 9 number symmetry:
The number 1 and every third triangular number thereafter form the 1+9+18+27+...(9n) additive series (1, 10, 28, 55, …). Each number in this additive series, aside from the first, is a multiple of 9. A concentric triangular arrangement of first 9, then 18, then 27 spheres (9n) about the first central sphere (first 1). This is why in modulus 9 all the numbers in this subset of ‘’1-like’’ triangles reduce to 1 (i.e. 1, 1, 1, 1, … mod 9).
The number 3 and every third triangular number thereafter form the 3+12+21+30+...(3+9n) additive series (6, 21, 45, 78, …). A concentric triangular arrangement of first 12, then 21, then 30 spheres (3+9n) about the first 3 central spheres. In modulus 9 the subset of these ‘’3-like” triangles alternate 3-6-9 (i.e. 3, 6, 9, 3, 6, 9, …) because each number in the additive series reduces to 3.
The number 6 and every third triangular number thereafter form the 6+15+24+33+...(6+9n) additive series (3, 15, 36, 66, …), which corresponds to the concentric triangular arrangement of first 15, then 24, then 33 spheres (6+9n) about the first 6 central spheres. In modulus 9 the subset of these ‘’6-like’’ triangles alternate 6-3-9 (i.e. 6, 3, 9, 6, 3, 9, …) because each number in the additive series reduces to 6.
Interleaved, these three triangular spherically close-packed planes form the continuous tetrahedral proportion, where the central sphere of 1-like triangles is cuboctahedrally coordinated by 12 surrounding spheres — hinting at its underlying complementary rotational symmetry.
That number admits nothing beyond the ennead (nine), but rather everything circles around within it, is clear from the so-called recurrences: there is natural progression up to it, but after it there is repetition. …so that it is by no means possible for there to subsist any number beyond nine elementary numbers.
Iamblichus
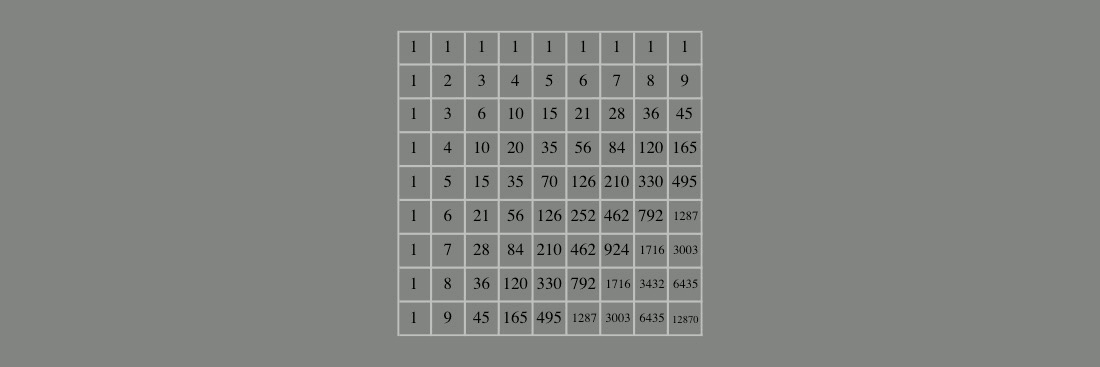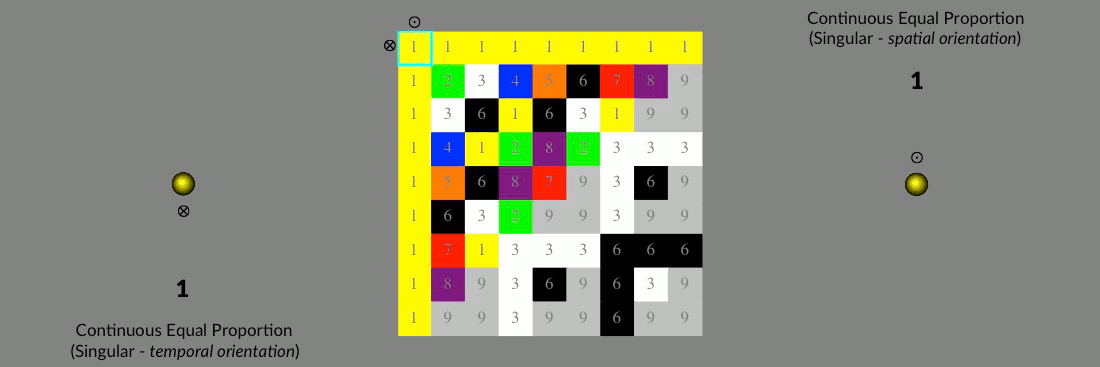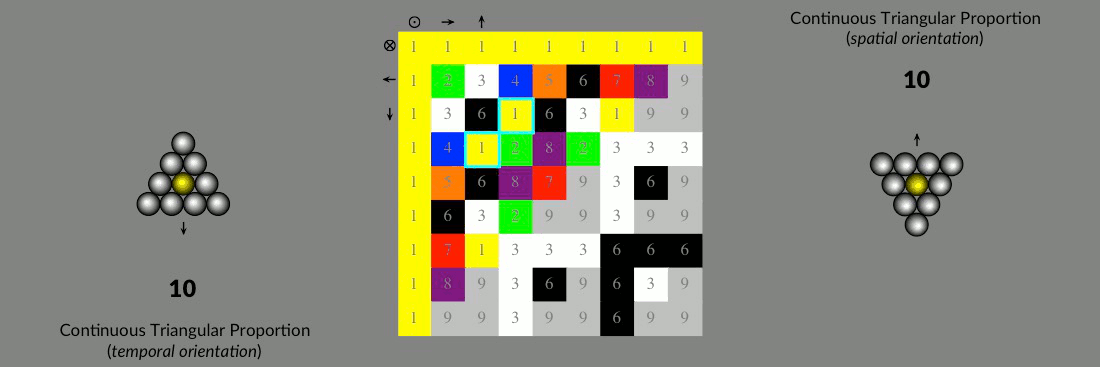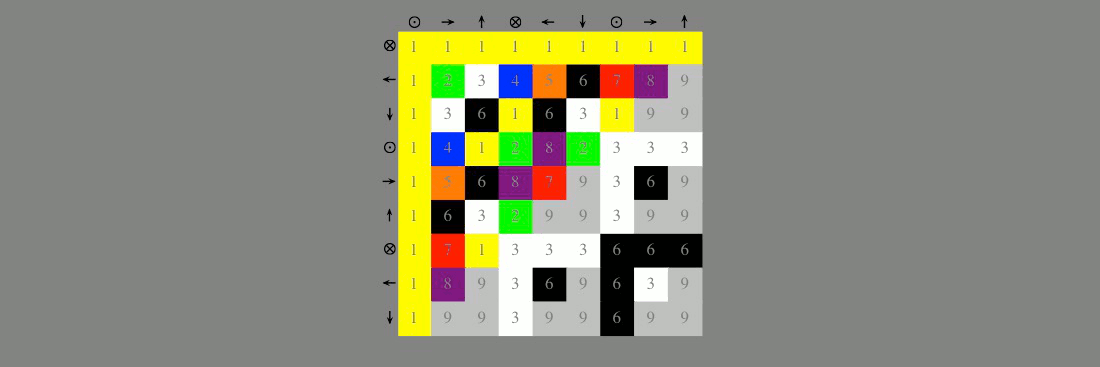
Pascal’s triangle, dimensional invariance, mod 9 and translational proportion…
With the next animation observe the underlying dimensional symmetry of Pascal’s triangle evolve. This figure is meant to accompany the content in Chapters 3 thru 6 of Natural Number.
The geometric constructs in the graphic demonstrate how succeeding columns and rows (translational proportion) are formed by summing their respective predecessor column or row at right angle. The figure also demonstrates the inverse (spatial vs. temporal) relationship between columns and rows.
Chapter 3 of Natural Number provides a geometric explanation for these relationships tied to the interplay of the germinal symmetry elements of point (1) and void (0) that sum as orthogonal vectors to perpetuate the continuous equal proportion of the singular dimensions of space and time.
Chapter 5 ties these succeeding sums of point and void to the incremental incorporation of modulus 9 numeric invariance within succeeding columns and rows, as evidenced by the incremental incorporation neutral 9s within each successor.
Taken together with the relative orientations of linear, triangular, and tetrahedral translational proportion, and the underlying geometric incorporation of nines, all observations are mutually consistent. This points to a repeating pattern of rotation between dimensional orientations, and a continued proportion may be characterized by a minimum of three terms: past, present, and future — thus establishing the dimensional continuum.
…there are some who say that there is a right and left of the heavens, as, for instance, those that are called Pythagoreans (for such is their doctrine).
Aristotle
Super-symmetric rotational proportion…
Use the animations below to study the complementary rotational symmetry transformations that accompany the continuous proportion of the diagonal intervals of Pascal’s triangle (Note: mirror temporal and temporal/spatial orientations not shown). These graphics are meant to accompany the content in Chapter 8 of Natural Number.
First tab: The continuous Geometrical Proportion of 1:1 diagonal sums (1, 2, 4, 8, 16, 32, …) is shown conforming to complementary cubic symmetry transformations —Transformations between complementary cube faces through rotation about the 3-6 cube-diagonal dipole axis of the complementary color cube. A super symmetry coordinated about the central spherical point or monad — the singular dimension. Note that this continuous cubic geometry is consistent with the relative orientation of dimensional constraints shown in the preceding example.
Second tab: The continuous Golden Proportion of 2:1 diagonal sums (1, 1, 2, 3, 5, 8, …) is shown conforming to complementary cuboctahedral symmetry transformations. Transformations between complementary octahedral faces through rotation about the octahedral-diagonal dipole axis corresponding to 1-8 cube faces of the complementary cuboctahedron. The continuous golden proportion can be considered the governing super-symmetric proportion of the field due to a symmetric hierarchy and sequential ordering of dimensional invariance requiring only the symmetric intent of point (1) and void (0) to establish the continuum. This governing spatial/temporal rotational super symmetry is coordinated about the central singular dimension and is the origin of the natural numeric order of the universe — the virtual dimensional symmetry of energy.